Best 20 Fits
Fit Result 1 for Cancer of the Lower GI Tract (1890s decade)
for European American Males (EAM)
m =2, n = 4
CAL(g) vs. Cell Doubling (g)
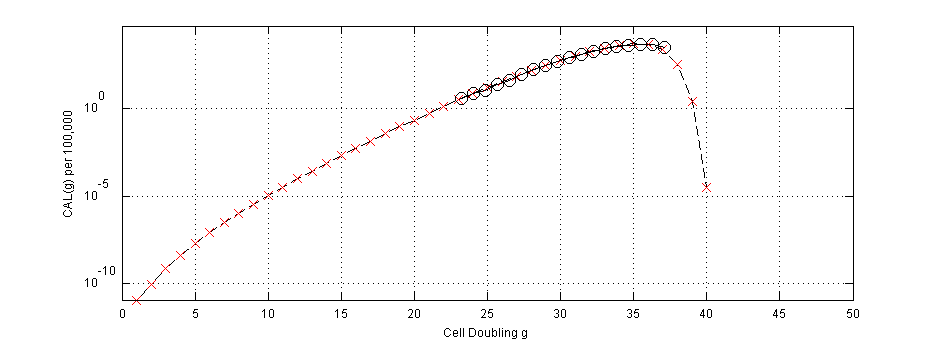
|
|||
| Linear-Linear Plot | Log-Linear Plot | CLOSEUP of Log-Linear Plot | Log-Log Plot |
CAL(t) vs. Age (t)

|
|||
| Linear-Linear Plot | Log-Linear Plot | CLOSEUP of Log-Linear Plot | Log-Log Plot |
Goodness of Fit
The values of INC(h,t) vary more than a thousand-fold among the 18 age of death intervals recorded from maturity to old age (Fig.1). Statistical comparison of CAL(h,t) to INC(h,t) required a term that gave weight to all 18 intervals. Such a term is |log10 CAL(h,t) - log10 INC(h,t)| which is zero when the terms are identical, i.e. their ratio is equal to 1.0. The square root of the average of the square of these 18 terms is here employed as a goodness of fit parameter, GOF(h,t).
GOF(h,t) = {SUM [log10 CAL(h,t) - log10 INC(h,t)]2 /18}1/2
GOF(h,t) may have practical meaning for the general reader as it is akin to a standard deviation of |log10 CAL(h,t)-log10 INC(h,t)| averaged over all adult life. If GOF(h,t) = 0.1 then the 95% confidence limits of the average ratio of CAL(h,t) /INC(h,t) would be 10-0.2 and 100.2 or 0.63 and 1.58. If GOF(h,t) = 0.03 the 95% limits would be 0.93 and 1.07. A GOF(h,t) of greater than 0.1 indicates a poor fit of the model with stipulated parameters “n” and “m” or marked errors in the values of INC(h,t) arising from either sampling error or bias. Errors arising from small sample sizes do not contribute significantly to GOF(h,t) when large U.S. European-American cohorts are studied.
Table of Results
| Fit Rank | Goodness of Fit GOF(h,t) | F_prom | F_init | f | mu | R_initiation | R_promotion | Area |
| 1 | 0.05221 | 1.000 | 0.127 | 1.000 | 0.163 | 6.579e-004 | 3.511e-003 | 0.246 |
| 2 | 0.07130 | 1.000 | 0.127 | 1.000 | 0.153 | 6.579e-004 | 4.329e-003 | 0.246 |
| 3 | 0.10326 | 1.000 | 0.127 | 1.000 | 0.174 | 6.579e-004 | 2.848e-003 | 0.245 |
| 4 | 0.12724 | 1.000 | 0.127 | 1.000 | 0.142 | 6.579e-004 | 5.337e-003 | 0.247 |
| 5 | 0.13217 | 1.000 | 0.127 | 1.000 | 0.163 | 6.579e-004 | 4.329e-003 | 0.246 |
| 6 | 0.14961 | 1.000 | 0.127 | 1.000 | 0.174 | 6.579e-004 | 3.511e-003 | 0.246 |
| 7 | 0.15045 | 1.000 | 0.127 | 1.000 | 0.153 | 6.579e-004 | 3.511e-003 | 0.246 |
| 8 | 0.15597 | 1.000 | 0.127 | 1.000 | 0.142 | 6.579e-004 | 4.329e-003 | 0.246 |
| 9 | 0.15831 | 1.000 | 0.127 | 1.000 | 0.153 | 6.579e-004 | 5.337e-003 | 0.247 |
| 10 | 0.17208 | 1.000 | 0.269 | 1.000 | 0.142 | 8.111e-004 | 2.848e-003 | 0.553 |
| 11 | 0.17332 | 1.000 | 0.127 | 1.000 | 0.184 | 6.579e-004 | 2.310e-003 | 0.245 |
| 12 | 0.17344 | 1.000 | 0.127 | 1.000 | 0.163 | 6.579e-004 | 2.848e-003 | 0.245 |
| 13 | 0.18298 | 1.000 | 0.269 | 1.000 | 0.132 | 8.111e-004 | 3.511e-003 | 0.554 |
| 14 | 0.18668 | 1.000 | 0.127 | 1.000 | 0.132 | 6.579e-004 | 6.579e-003 | 0.247 |
| 15 | 0.18797 | 1.000 | 0.127 | 1.000 | 0.132 | 6.579e-004 | 5.337e-003 | 0.247 |
| 16 | 0.18911 | 1.000 | 0.269 | 1.000 | 0.153 | 8.111e-004 | 2.310e-003 | 0.552 |
| 17 | 0.19601 | 1.000 | 0.269 | 1.000 | 0.153 | 8.111e-004 | 2.848e-003 | 0.553 |
| 18 | 0.20406 | 1.000 | 0.269 | 1.000 | 0.163 | 8.111e-004 | 2.310e-003 | 0.552 |
| 19 | 0.20496 | 1.000 | 0.269 | 1.000 | 0.142 | 8.111e-004 | 3.511e-003 | 0.554 |
| 20 | 0.20583 | 1.000 | 0.127 | 1.000 | 0.184 | 6.579e-004 | 2.848e-003 | 0.245 |